International Journal of Nanomaterials, Nanotechnology and Nanomedicine
Fullerene and nanotube models in Bolyai - Lobachevsky hyperbolic geometry H3 on the 200th anniversary of its discovery
Emil Molnár* and Jenő Szirmai
Cite this as
Molnár E, Szirmai J (2023) Fullerene and nanotube models in Bolyai - Lobachevsky hyperbolic geometry H3 on the 200th anniversary of its discovery. Int J Nanomater Nanotechnol Nanomed 9(1): 004-005. DOI: 10.17352/2455-3492.000050Copyright License
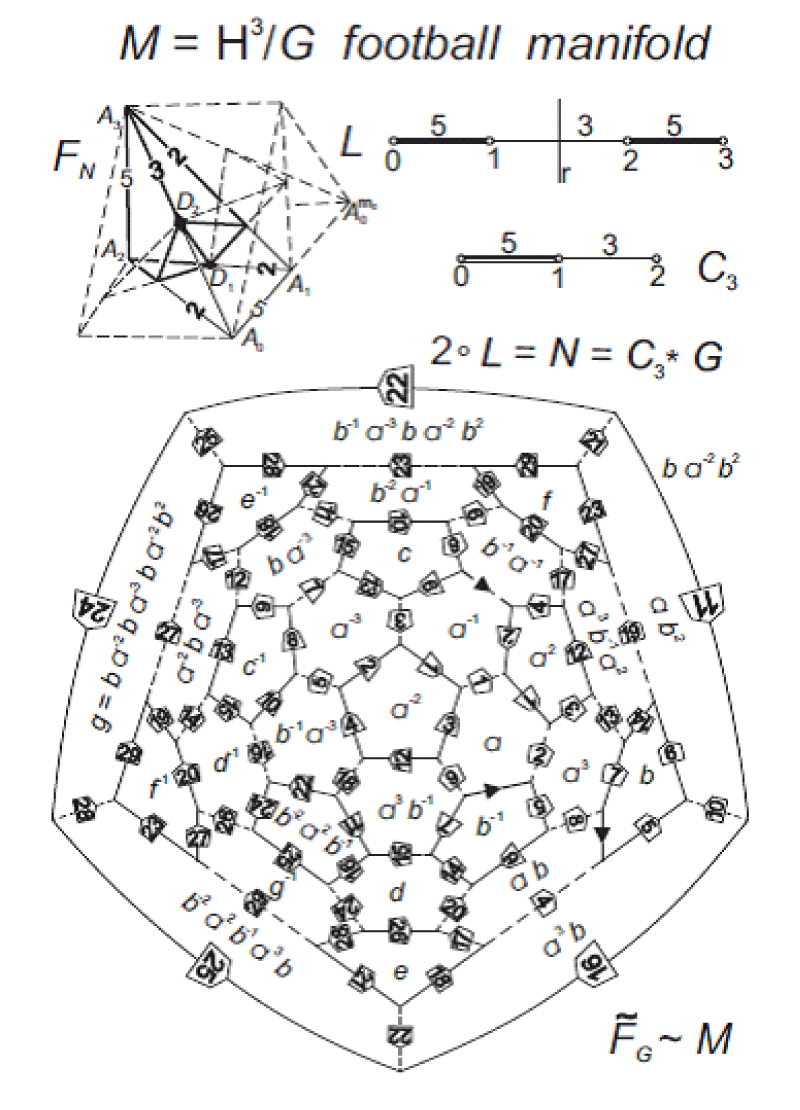
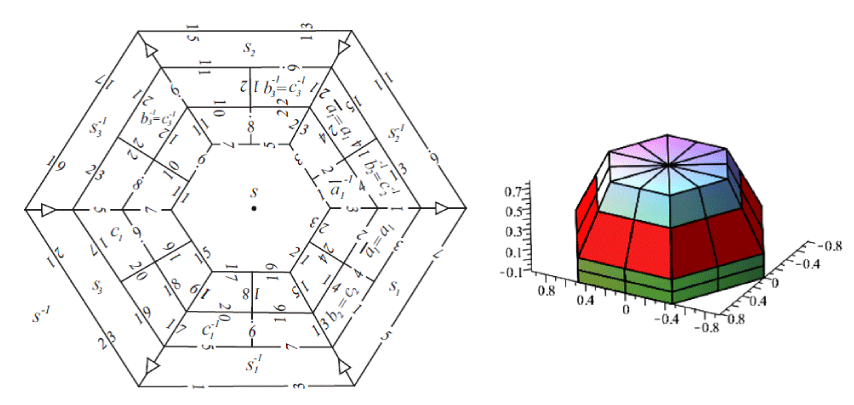
© 2023 Molnár E, et al. This is an open-access article distributed under the terms of the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original author and source are credited.The Archimedean solid (5, 6, 6), where regular pentagon, hexagon and hexagon surround each vertex, so altogether 60 vertices (with carbon atoms for C60 fullerene). 12 pentagons and 20 hexagons bound this football polyhedron, as a regular (say white) icosahedron truncated by 12 (black) pentagons at its 12 vertices. But now (Figure 1) we consider this as a fundamental polyhedron F with paired side faces for a hypothetic (for a while) future space tiling FG under a space group G, generated by the face pairing mappings ([1,2] for analogous constructions).
In the following necessary technical explanation (which can be skipped at first glance, see only the summarizing diagram (1)), first we start with this face pairing at the 3 → (arrow) edges: a: a-1 --> a means that the motion maps the hexagon face a-1 (with 1st →) onto hexagon face a (with 2nd →) and polyhedron F onto its a-image Fa in the other half-space of a; a-1: a --> a-1, F --> Fa-1 define inverse generator. Then take the other face on F at this 2nd → as pentagon b-1 and its image pentagon face b at the third → and the motion b: b-1 --> b as before, also with Fb. As a result, we obtain at the 3rd → the face ab, then at the 1st →, face b-1a-1, thus ab: b-1a-1 --> ab and Fab can also be obtained by our convention. This also means that the edge → are surrounded by 3 polyhedra in the fundamental space tiling FG.
G∋ g is a product of generators a, b (and or their inverses). Fag is adjacent to Fg at the image face ag, as a general rule.
Look at our Figure 1, where we see our lucky situation: after having assigned the 3 → edges and generator motions a and b, we can finish the side face pairing on the fundamental polyhedron F as identity domain F1, by introducing new and new edge tripples and getting either new face pairing expressed by a and b, or we get trivial relation, or non-trivial, so-called defining relation for the future fundamental group G. The first new edge tripple is denoted by 1 also as a type of arrow between faces a-1 and a, introducing a2 and its inverse a-2. In the end, we have obtained 30 edge tripples (the last one is 29) with two essential defining relations to the two generators a and b. For details, [1,2]. It turns out that we have 15 G-equivalence classes of the 60 vertices, 4 vertices in each class. From any vertex 4 edge classes start or end as at carbon atoms. It seems that C15 would be a better notation instead of C60.
This construction was published first in [3] in 1988, as a hyperbolic football manifold (without any fullerene reference). For our other results, partly joint with István PROK, e.g. [1,2] and our didactical introductory paper [4] is extremely advised. The existence in hyperbolic space H3 is based on the generalized projective Beltrami-Cayley-Klein model of H3 also described in [1,2] and summarized below.
The left upper part of Figure 1 shows the so-called characteristic simplex A0A1A2A3, spanned by basis vectors a0, a1, a2, a3 of a real 4-dimensional (left) vector space V4. A usual vector x = xiai (with Einstein-Schouten index conventions) and its real multiple cx ~ x express the same point, X. The side face bi, opposite to Ai, is expressed by the linear form bi of the (right) dual form space V4 by aibj = δij (Kronecker delta symbol), as usual.
Now for our football manifold, the face angles of the characteristic simplex C (5, 3, 5) are specified by formal symmetric bilinear scalar product (of future signature (+, +, +, – )) as follows (by the so-called Coxeter (ortho-scheme) diagram upper right of Figure 1):
< bi, bj > = – cos (bibj), with convention angle (bibi), where < b0, b1 > = < b2, b3 > = – cos pi/5, <b1, b2 > = – cos pi/3, < b0, b2 > =
Here the half-turn symmetry r (0 ↔3, 1↔2), the reflections mi in side face bi (i = 0, 1, 2, 3) of the characteristic simplex also play important roles. The signature of this scalar product is (+, +, +, – ), indeed [1,2]! This involves the general angle metric. Its inverse scalar product (with the same signature) involves the general distance metric. Then inscribed ball, circumscribed ball, and densities of ball packing and covering can be computed, with better values than in Euclidean cases. The "only" task is to fill out the football tiling with materials under the "football group" G given above by generators and defining relations [1,3].
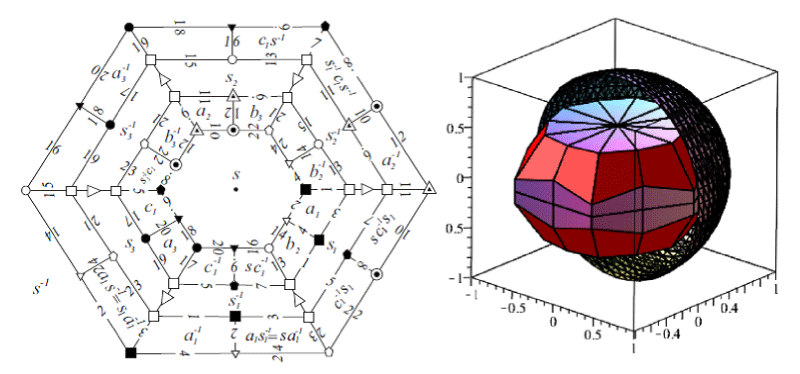
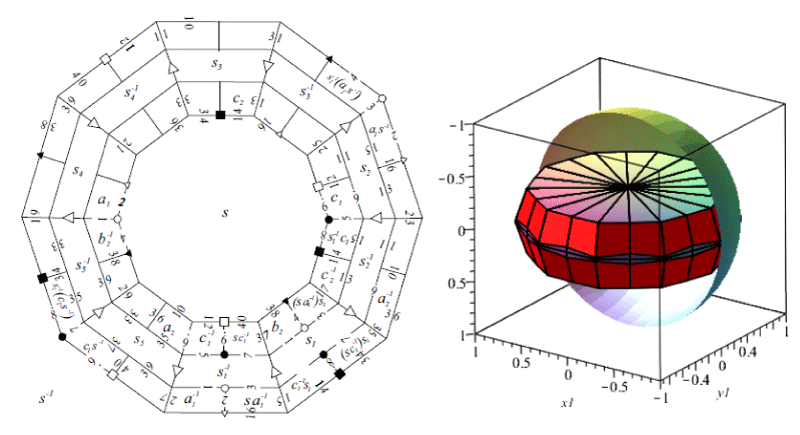
Our other initiative is the infinite series of nanotube models that are completely analogous. Only the characteristic simplex C (2z, 2z, 2z, 3 ≤ z odd) (in Figure 2, 4 z = 3 in two equivalent interpretations), but z = 5 (Figure 3), 7 are also simple) will be doubly truncated (by polar planes of A0 and A3) in the hyperbolic sense and its half part will be taken as in our recent paper [2] (to be continued). The prism-like fundamental polyhedron has two base planes paired by an appropriate z-screw motion, so we obtain an infinite tube. The side faces cause a screw structure of tubes with z-rotational symmetry. Our investigations with this tube manifold structures are going on.
- Molnár E. On non-Euclidean crystallography, some football manifolds, Strctural Chemistry. 2012; 23:1057-1069. DOI 10. 1007/s11224-012-0041-z.
- Molnár E, Szirmai J. Infinite series of compact hyperbolic manifolds as possible crystal structures, Matematički Vesnik. 2020; 72:3; 257-272.
- Molnár E. Two hyperbolic football manifolds, Proceedings of International Conference on Differential Geometry and Its Applications, Dubrovnik Yugoslavia. 1988; 217-241.
- Molnár E, Prok I, Szirmai J. From a nice tiling to theory and applications, Editors: Zdenka Kolar-Begović, Ružica Kolar-Super, Ljerka Jukic Matić, Towards New Perspectives on Mathematics Education, Mathematics and Children. Josip Juraj Strossmayer University of Osijek. 2019; 85-106.

Article Alerts
Subscribe to our articles alerts and stay tuned.
 This work is licensed under a Creative Commons Attribution 4.0 International License.
This work is licensed under a Creative Commons Attribution 4.0 International License.
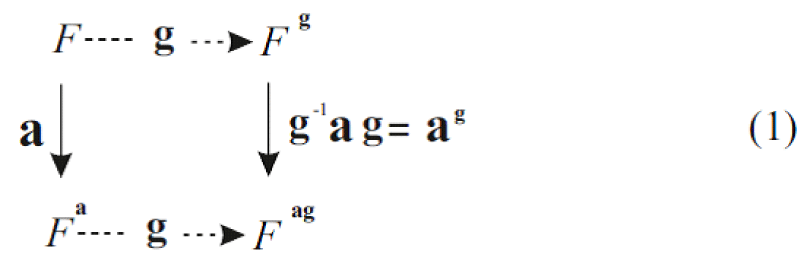
 Save to Mendeley
Save to Mendeley
